Generally I work in the intersection of algebra and topology. I am motivated by questions arising from knot theory, but I prefer to give algebraic answers to the questions. I like to study maps between things, so I am naturally drawn to representation theory (mostly of the braid groups), finite type invariants, planar algebras, and quantum computing.
Here is my CV.
Here is a link to my ArXiv papers.
Here are my papers:
 Danceability, a new definition of bridge index joint with Sol Addison, Lila Snodgrass and Everett Sullivan
Danceability, a new definition of bridge index joint with Sol Addison, Lila Snodgrass and Everett Sullivan
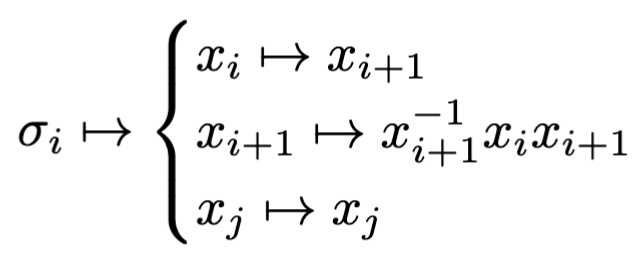
Searching for Order Preserving Braids Algorithmically joint with Jonathan Johnson and Hannah Turner
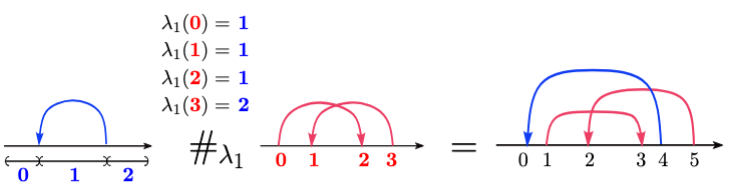 Computing Finite Type Invariants Efficiently join with Dror Bar-Natan, Itai Bar-Natan and Iva Halacheva
Computing Finite Type Invariants Efficiently join with Dror Bar-Natan, Itai Bar-Natan and Iva Halacheva
Danceability,_Directed_by_Braid_Index_ joint with Sol Addison and Lila Snodgrass
 The quotients of the Braid Groups by Their Congruence Subgroups joint with Wade Bloomquist and Peter Patzt
The quotients of the Braid Groups by Their Congruence Subgroups joint with Wade Bloomquist and Peter Patzt
![]()
Large 1-Systems of Curves in Non-Orientable Surfaces joint with students Sarah Ruth Nicholls and Julie Shneidman as part a summer REU project.
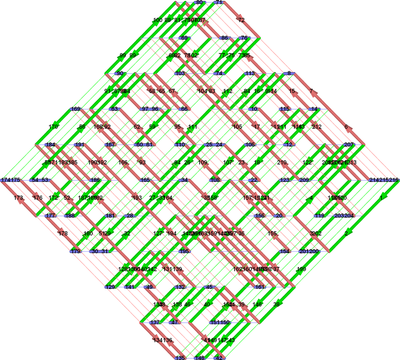
Yarn Ball Knots and Faster Computations, joint with Dror Bar-Natan, Itai Bar-Natan and Iva Halecheva
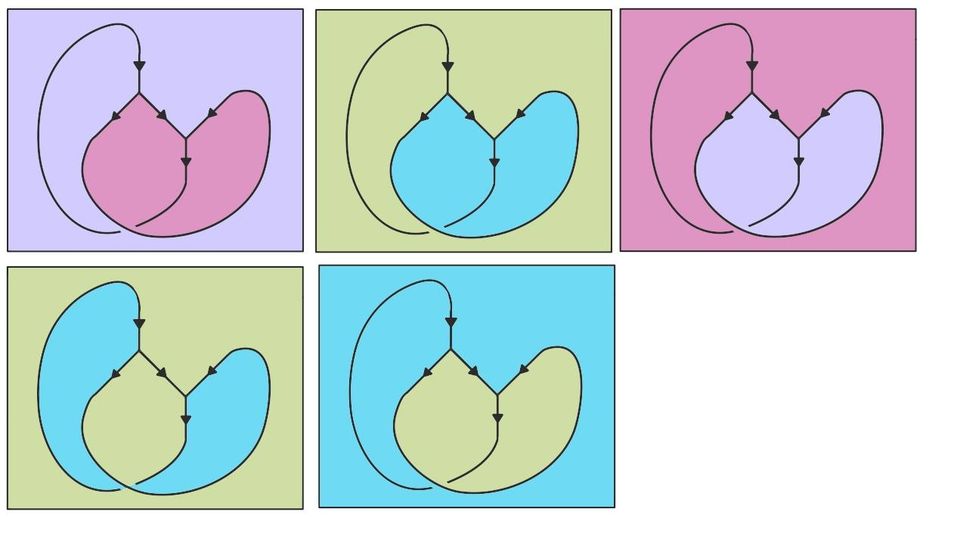
An Invariant of Virtual Trivalent Spatial Graphs, joint with Sherilyn Tamagawa and Evan Carr
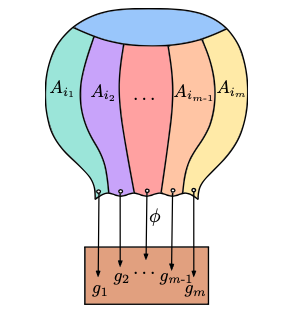
Finite Image Homomorphisms of the Braid Group and its Generalizations Joint with Yvon Veberne
OC relation— A quick proof of a known fact that the OC relation can be written in two ways.

Ribbon 2-Knots, 1+1=2, and Duflo’s Theorem for Arbitrary Lie Algebras joint with Dror Bar-Natan and Zsuzsanna Dancso
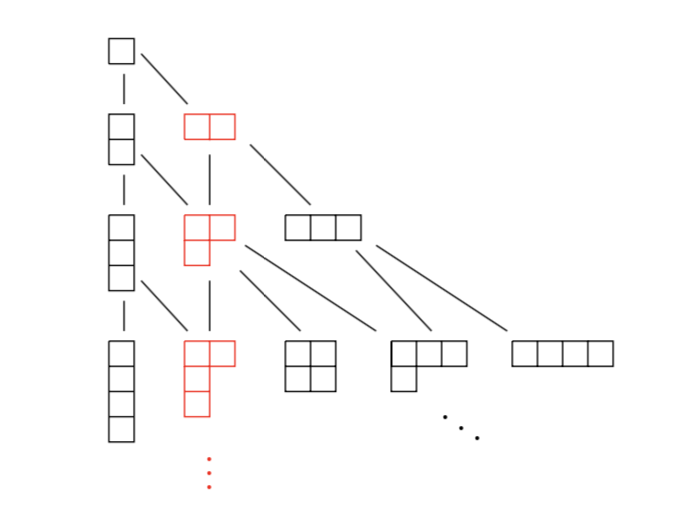
PhD Thesis: Discrete Representations of the Braid Groups
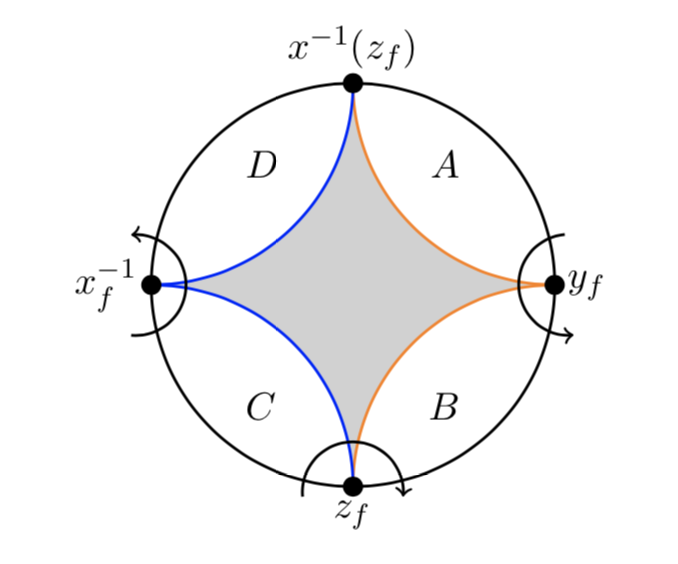
Complete Classification of Discrete Specializations of the Burau Representation of B_3

A Survey of Grid Diagrams and a Proof of Alexander’s Theorem
My Master’s thesis: The Alexander Polynomial

Turning Math Into Dance: Lessons from Dancing my PhD
